What is calculus?

By carefully reading this section, you will acquire a basic understanding of what you will be learning in your first two semesters of calculus: the central themes and types of problems that calculus allows engineers, mathematicians, and scientists to solve. It gives you a preliminary answer to the question, “What is calculus?” When you finish the two courses, your comprehension of this answer will be deeper and more detailed.

Differential Calculus. The central concept of the first-semester college calculus course covered in chapters 1–4 is that of defining the slope of a curve. You begin this course knowing from algebra that the slope of a line is defined as rise over run. In differential calculus you learn how to extend the rise over run definition so that it gives the slope of a curve, a shape that changes at every point. If you draw a simple curve such as the one below and trace along it with your hand pointing in the direction of the curve at each point, you will see the slope of the curve:

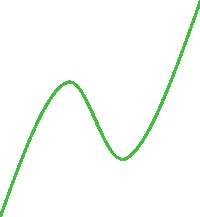
The slope is the direction in which your hand is pointing at each point on the curve. We will come up with a definition of the slope of a curve, called the derivative, that gives that direction at each point on the curve. Notice that as we move from left to right the curve rises to a peak, falls to a trough, and then rises again.

You might be wondering, “What is a curve, and why are we studying curves instead of lines?” Suppose you work for a company that manufactures contact lenses. Designing contact lenses of the correct shape requires a thorough understanding of curves and of the functions that characterize them. Your contact lens manufacturer employs a team of programmers and scientists that uses lasers to cut each lens to the shape of the curve that improves the vision of your eyes.

The peaks and troughs on a curve are the points that are particularly important in defining a curve and in making objects characterized by a curve, like a contact lens. Calculus allows us not only to find the shape of a curve but also the peaks, troughs, and special points where its shape changes, called inflection points. In the curve above, there is an inflection point about halfway down the falling section. To the left of this point, the curve has a downward shape; to the right, it has an upward shape.

Integral Calculus. The second semester of calculus covered in chapters 5–8 teaches you how to use integrals, or anti-derivatives, in application problems to find the area under or between curves. Ancient Greek mathematicians knew how to find the area of an irregularly shaped region by breaking it down into smaller known sections whose summed area approximately equaled the whole. In finding areas using integrals, mathematicians extend the ancient Greek approach, which allows us to find many irregular areas exactly. Finding exact answers using derivatives or integrals requires finding limits, a core notion in calculus. Limits allow us to get as close as needed to an exact answer. The paradox is—thanks to the genius of mathematicians like Newton and Riemann—that when we are close enough we actually do have an exact answer, which is known as an exact or closed form solution. Thus, limits in calculus are variants of the philosopher Zeno of Elea’s timeless paradox posed in the fifth century B.C.E.: “If you move half the distance to an object each time you move, will you ever reach it?” No, you will not, but you will eventually be so close that you are essentially there, as is the case with answers found using limits.

Integrals also allow us to determine the length of a portion of a curve, which is much more difficult than determining the length of a line segment, as well as to calculate such application problems as determining a volume, the center of mass of an object, or the pressure against a submerged object (such as the wall of a dam).

For instance, suppose you are designing gold earrings shaped as below. If the top and bottom conform to the shape of a specific curve, using calculus you can calculate the amount of gold each earring requires (assuming uniform thickness) and thereby determine the material cost.

Or, suppose you are designing art objects in the shape of a specific function rotated around an axis to create a volume, as below. With integral calculus you can compute that volume, allowing you to calculate material needs. In any process in which objects of intricate irregular shapes are used, integrals allow us to calculate their volumes.

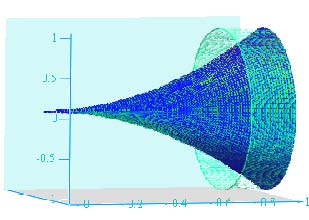
In an engineering application, you might need to know the balance point of an irregularly-shaped piece of material so that you can balance it with minimal or no side suspension. The balance point, called the center of mass, can be determined using integral calculus techniques.

y

x

As discussed, using calculus techniques we can often find exact answers. But in practice it is often too difficult, too time-consuming, or even impossible to find exact solutions. Fortunately, using calculus techniques with computers, we can find approximate solutions that are almost always as accurate as needed. Throughout the book, approximate solutions are highlighted by an approximation symbol (~), to contrast these with exact or closed form solutions.

In the chapters ahead, you will be working to understand not just the technical details of each section (the how) but why and when calculus techniques are needed—and so why calculus is important and what it is about. Bright-yellow text boxes labeled The Professor Says found in most sections are designed to light your way. They answer the recurring question, “Why is this technique needed and when is it used?”

It may take a week or more for the concept of a given section to sink in. Think of yourself in good calculus fashion as getting closer and closer to understanding with each step in the learning process: actively listening to the class lecture, working your way through this textbook, doing the homework, reviewing your homework, and studying for exams. Take advantage of what many studies have shown: Studying in a group results in more solid learning and in better grades for most people, particularly those for whom the material does not come easy. The peer critique of group studying deepens your understanding as you practice verbalizing concepts, and it builds your proficiency as you critique each other’s techniques.

Enjoy the challenge that awaits you!